고정 소수점(fixed point)과 부동 소수점(floating point)

요즘 자바의 기초를 다시 공부하고 있다. 자바의 기초, 특히 변수에 대해서 공부하다보면 다양한 기본 자료형이 나오는데, 그 중에서 실수형을 다루는 float와 double에 나오는 개념인 고정 소수점과 부동 소수점에 대해 알아보고자 한다. 고정 소수점, 부동 소수점은 어떤 개념일까? 그에 앞서 실수형 자료형인 float와 double에 대해서 알아보자.

실수형 - float, double

실수형의 범위와 정밀도

실수형에는 대표적으로 4byte의 자료형 float와 8byte의 자료형 double이 존재한다. 이 둘의 범위와 정밀도를 비교하면 아래와 같다.

타입	저장 가능한 값의 범위	정밀도	크기 - byte(bit)
float	-3.4 x 10³⁸ ~ -1.4 x 10⁻⁴⁵, 1.4 x 10⁻⁴⁵ ~ 3.4 x 10³⁸	7자리	4(32)
double	-1.8 x 10³⁰⁸ ~ 4.9 x 10^³²⁴, 4.9 x 10⁻³²⁴ ~ 1.8 x 10³⁰⁸	15자리	8(64)

실수형은 소수점까지 표현해야 하므로 '얼마나 큰 값을 표현할 수 있는가'뿐만 아니라,
'얼마나 0에 가깝게 표현할 수 있는가'도 중요하다.

여기서 등장하는 개념이 오버플로우와 언더플로우이다. 오버플로우와 언더플로우란 무엇일까?

오버플로우

표현 범위의 최댓값을 벗어났을 때 발생하는 것으로 실수형에서는 무한대(infinity)가 된다.

언더플로우

실수형으로 표현할 수 없는 아주 작은 값으로, 양의 최소값보다 작은 값이 되는 경우를 뜻하는데 이때 변수의 값은 0이 된다.

int보다 float가 훨씬 큰 값을 표현할 수 있는 이유

그런데 크기를 살펴보면 int(4byte), float(4byte)이다. 어떻게 같은 4byte로 int보다 훨씬 큰 값을 표현할 수 있을까? 이는 값을 저장하는 형식이 다르기 때문이다.

표현 방식

int: 1 + 31 = 32(4byte)

float: 1 + 8 + 23 = 32(4byte)

float 타입과 같은 실수형은 부호(S), 지수(E), 가수(M) 세 부분으로 이루어져 있다. 즉, 2의 제곱을 곱한 형태( ± M x 2ᴱ)로 저장하기 때문에 큰 범위의 값을 저장할 수 있다.

하지만 장점만 존재하는 것은 아니다. 정수형과 달리 실수형은 오차가 발생할 수도 있다는 단점이 존재한다. 그렇기 때문에 실수형에는 '정밀도(precision)'가 중요한 요소이다. float 타입의 예를 들어보겠다. float 타입은 정밀도가 7자리이다. 즉, a x 10ⁿ(1≤a<10)의 형태로 표현된 ‘7자리의 10진수를 오차없이 저장할 수 있다’는 의미이다. 그렇기 때문에 float와 double을 비교하면 아래와 같이 볼 수 있다.

연산속도의 향상이나 메모리를 절약하려면 float,
더 큰 값의 범위나 더 높은 정밀도가 필요하면 double

예시 코드와 함께 알아보자. 다음 코드는 float와 double을 자바에서 표기한다.

public static void main(String[] args) {
        float f = 9.12345678901234567890f;
        float f2 = 1.2345678901234567890f;
        double d = 9.12345678901234567890d;

        System.out.printf("      123456789012345678901234%n");
        System.out.printf("f  :    %f%n", f); // 소수점 이하 6번째 자리까지 출력
        System.out.printf("f  :  %24.20f%n", f);
        System.out.printf("f2 :  %24.20f%n", f2);
        System.out.printf("d  :  %24.20f%n", d);
    }
}

위 코드를 실행하면 결과는 다음과 같다.

// 실행결과
123456789012345678901234
f  :    9.123457
f  :    9.12345695495605500000
f2 :    1.23456788063049320000
d  :    9.12345678901234600000

아마 부동 소수점과 고정 소수점을 처음 접하는 사람들은 왜 이런 결과가 나왔는지 이해하지 못할 것이다.

이렇게 출력되는 이유는 실수형의 저장형식과 관련이 있다. 이제 실수형의 저장형식을 알아보자.

실수형의 저장형식

± M x 2ᴱ

실수형의 저장형식은 위 수식과 같다. 다음 표에서 수식을 설명한다.

기호	의미	설명
S	부호(Sign bit)	0이면 양수, 1이면 음수
E	지수(Exponent)	부호있는 정수. 지수의 범위 : -127 ~ 128(float), -1023 ~ 1024(double)
M	가수(Mantissa)	실제값을 저장하는 부분. 정밀도 : 10진수로 7자리(float), 15자리(double)

실수는 위 표와 같이 부호, 지수, 가수로 구성된다.

부호(Sign bit)
- 부호비트를 의미하며 1 bit의 크기를 가진다. 0이면 양수, 1이면 음수를 의미한다. 2의 보수법을 사용하지 않는다.
지수(Exponent)
- float의 경우 8 bit의 크기를 가지며 지수는 부호있는 정수이고 8 bit의 크기로 모두 2⁸(=256)개의 값을 저장할 수 있으므로 -127~128의 값이 저장된다.
- 이 중에서 -127과 128은 숫자가 아니며(NaN; Not a Number), 양의 무한대, 음의 무한대와 같이 특별한 값의 표현을 위해 예약되어 있어 실제 사용 가능한 지수의 범위는 -126~127이다.
  - float 타입으로 표현할 수 있는 최대값 = 2¹²⁷ ≒ 10³⁸
  - (가수의 마지막 자리가 2⁻²³이므로 지수의 최소값보다 2⁻²³ 배나 더 작은 값)최소값 = 10⁻⁴⁵
가수(Mantissa)
- M의 실제 값이 가수를 저장하는 부분이다.
- float는 2진수 23자리를 저장할 수 있다. 따라서 약 7자리의 10진수를 저장할 수 있는데 이것이 float의 정밀도를 뜻한다.
- double은 2진수 52자리를 저장할 수 있다. 이는 float보다 약 2배의 정밀도를 가지고 있다.

이제 위의 예시에서 예상치 못한 오차가 발생한 근본적인 이유를 설명하겠다. 이는 정규화라는 개념과 관련 있다.

정규화

부동 소수점에 오차가 발생하는 이유는 다음과 같다. 실수 중에는 무한 소수(ex. 𝜋)가 존재한다. 그리고 실수는 10진수가 아닌 2진수로 저장을 하기 때문에 10진수로는 유한소수여도 2진수로 변환 시 무한소수가 되는 경우가 존재한다. 위의 예시에서 나왔던 10진수인 9.1234567을 2진수로 변환해보자.

9.1234567 → 1001.000111111001101011011011…₍₂₎

→ 2진수로 변환된 실수를 저장할 때는 먼저 ‘1.xxx X 2ⁿ’의 형태로 변환되는데 이 과정을 정규화라고 한다.

위와 같이 2진수로 변환하게 되면 무한소수가 된다. 정규화된 2진 실수는 항상 1.으로 시작하기에 1.을 제외한 23자리의 2진수가 가수(mantissa)로 저장되고 그 이후는 잘려나간다. 지수는 기저법으로 저장되기 때문에 지수인 3에 기저인 127을 더한 130이 2진수로 변환되어 저장된다. 10진수 130은 2진수로 10000010이다.

기저법이란?
‘2의 보수법’처럼 부호있는 정수를 저장하는 방법. 저장 시 특정값(기저)을 더하고 읽어올 때 다시 뺀다.

이 때 잘려나간 값들에 의해 발생할 수 있는 최대오차는 약 2⁻²³인데, 이 값은 가수의 마지막 비트의 단위와 같음.

2⁻²³은 10진수로 0.0000001192(약 10⁻⁷)이므로 float의 정밀도가 7자리(소수점 이하 6자리)라고 한다.

이제 다음으로 9.1234567을 floatToBits() 메서드를 이용하여 16진수로 출력해보자. 여기서 floatToBits() 메서드는 float 타입의 값을 int 타입의 값으로 해석해서 반환하는 메서드이다.

public class _09_FloatToBinEx {
    public static void main(String[] args) {
        float f = 9.1234567f;
        int i = Float.floatToIntBits(f);

        System.out.printf("%f%n", f);
        System.out.printf("%X%n", i); // 16진수로 출력
    }
}

결과값이 예상이 되는가? 결과값은 아래와 같다.

9.123457
4111F9AE

이런 결과값이 나오는 이유를 설명하겠다.

우선 float 타입의 f부터 살펴보자. 9는 2진수로 1001로 바꿀 수 있고 소숫점 아래에는 0.1234567이 존재한다.

0.1234567은 .0001111111001101011011011…와 같이 무한소수로 이어진다. 따라서 이 둘을 합쳐서 2진수로 변환하면 다음과 같은 무한소수가 발생하게 된다.

9.1234567 → 1001.000111111001101011011011…

이 숫자를 위에서 언급한 정규화 과정을 거치면 어떻게 될까? 앞서 언급했듯이 1.을 제외한 23자리의 2진수가 가수로 저장되고 그 이후는 잘려나간다. 전반적인 변환 과정을 살펴보면 다음과 같다.

이때 반환된 값을 16진수로 출력하면, float 타입의 값이 2진수로 어떻게 저장되는지 확인할 수 있다.

그 실행 결과는 0x4111F9AE이다. 이런 결과값이 나오는 이유는 잘려나간 첫 번째 자리의 값이 1이기 때문에 반올림되어 0x4111F9AD의 2진수 마지막 자리 두 자리의 값이 01에서 10으로 1 증가했기 때문이다.

한번에 이해하기 어려운 개념이므로 그림으로 보충설명을 하겠다.

green : 부호비트(signed bit) / blue : 지수부(exponent) / red : 가수부(fraction / mantissa)

10진수를 2진수로 변환 그리고 정규화 과정 : 7.625 → 111.101₍₂₎ →(정규화)→ 1.11101 x 2²
부호비트 : 0(양수), 1(음수)
가수부(23자리) : 정규화 결과 소수점 오른쪽에 있는 숫자들을 왼쪽부터 그대로 넣고 남은 자리는 0으로 채움.

(소수점 왼쪽은 정규화를 하면 무조건 1이기 때문에 신경쓰지 않고 표현도 하지 않음. 이 1을 hidden bit이라 함)

지수부(8자리) : 2ⁿ에서 n에 해당하는 수인 2를 2진수로 바꾼 10’을 넣으면 될 것 같다.IEEE 표준에서 32 bit 를 사용하는 경우 bias 는 127이라 규정한다.→ 결론적으로 7.625는 컴퓨터에서 아래와 같이 저장된다.
→ 따라서 2 + 127 = 129를 2진수로 바꾼 10000001이 들어간다.
하지만 IEEE 표준에 따라 지수를 그대로 넣는 것이 아닌 ‘bias’ 라고 하는 지정된 숫자를 더한 다음 넣는다.

bias 값을 쓰는 이유에 대해 궁금할 수 있다. bias 값은 지수가 음수도 될 수 있기에 사용한다. 예를 들어보자.

0.000101₍₂₎ →(정규화)→ 1.01 x 2⁻⁴

만약에 bias가 없어서 2를 00000010₍₂₎ 으로 저장했다면 -4는 어떻게 저장할 것인가?

부호 비트는 지수의 부호와 관계 없고 지수용 부호 비트를 따로 만들기는 복잡하다.

따라서 8자리의 bit로 음수와 양수를 둘 다 표현하기 위한 방안을 마련하였다.

10진수 기준
0 ~ 127 : 음수
128 ~ 255 : 양수

(참고 : 실제로 0과 255는 0이나 0에 한없이 수렴하는 작은 수들, 무한대, NaN(Not a Number)과 같은 것들을 표현하기 위해서 특별하게 저장되어 있기 때문에 일반적인 표현 범위에 포함되지 않으며, 저런 수들을 표현할 때는 이 글에서 설명한 정규화 방법이 적용되지 않음)

다음으로 실수 표현 방식의 종류를 알아보자.

실수 표현 방식의 종류

실수는 언급했던 가수부와 지수부로 구성된다.

가수부와 지수부
- 가수부 : 2라는 숫자 부분을 보통 가수부라고 한다.
- 지수부 : 128이라는 수학적 표현에서 제곱의 위치에 해당한다.

이제 이 글의 주제이며 실수 표현 방식인 고정 소수점 방식과 부동 소수점 방식을 알아보겠다.

고정 소수점(fixed point) 방식

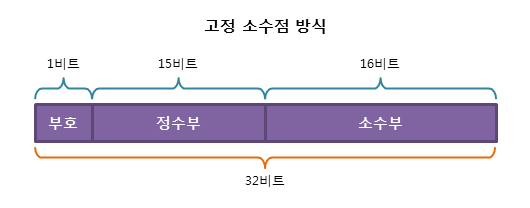
32 bit CPU에서 고정 소수점 방식을 실수로 표시하면 그림과 같다. 이 방식은 정수부와 소수부의 자릿수가 크지 않으므로 표현할 수 있는 범위가 매우 적으며 정밀도가 낮다는 단점이 있다. 7.625를 2진수로 변환해보자.

2진수로 변환하면 111.101₍₂₎이 된다. 이때 맨 앞 1자리는 0(양수) 또는 1(음수)이다.
소수점의 위치는 미리 정해두며 나머지 비트들은 소수점을 기준으로 정수부와 소수부를 표현하는 비트로 나눈다.
마지막으로 남는 뒷자리는 다 0으로 채운다.

이와 같이 표현되기에 고정 소수점 방식은 높은 정밀도가 필요없는 소규모 시스템에만 사용된다.

고정 소수점 방식은 구현하기 편리하지만 사용하는 비트 수 대비 표현 가능한 범위와 정밀도가 낮음 높은 정밀도가 필요 없는 소규모 시스템에서 간혹 사용됨

부동 소수점(floating point) 방식

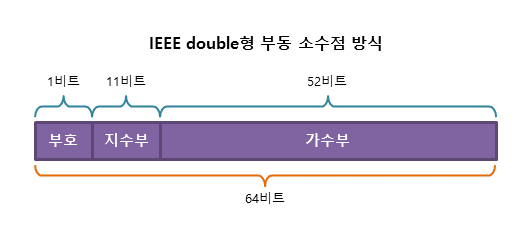
실수는 보통 정수부와 소수부로 나누지만, 가수부와 지수부로 나누어 표현할 수 있다. 부동 소수점 방식은 실수를 아래 식으로 표현한다.

± M x 2ᴱ⁻¹²⁷

이때 M의 범위는 1 ≤ M <2 인 실수이다.

고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작다. 하지만 부동 소수점 방식은 위의 수식을 이용하여 매우 큰 실수까지도 표현할 수 있다. 그렇기 때문에 현재 대부분의 시스템에서는 부동 소수점 방식으로 실수를 표현할 수 있다.

부동 소수점 방식의 오차

부동 소수점 방식은 항상 오차가 존재한다는 단점이 존재한다. 이러한 단점이 존재하는 이유는 무엇일까?

± M x 2ᴱ⁻¹²⁷ 공식을 사용하면 표현할 수 있는 범위는 늘지만, 10진수를 정확하게 표현할 수 없기 때문이다.

무한소수, 순환소수의 경우 가수부가 표현할 수 있는 비트 수를 넘어가게 되면 손실되는 부분이 생긴다.
실수 또한 이진수로 표현하기 때문에 가수부가 (½)²꼴로 표현되는 경우에만 오차없이 계산이 가능하다.

0.1을 1000번 더한 합계를 출력하는 예시를 통해 알아보겠다.

public class FloatingPointEx {
    public static void main(String[] args) {
        double num = 0.1;
        for(int i = 0; i < 1000; i++) {
            num += 0.1;
        }
        System.out.println(num);
    }
}

위 수식을 실행하면 어떤 결과가 예상되는가? 실행 결과는 아래와 같다.

100.09999999999859

0.1을 1000번 더한 합계는 계산하면 100이 되어야 하지만 실제로는 100.09999999999859가 출력된다. 이는 컴퓨터에서는 실수를 가지고 수행하는 모든 연산에서는 언제나 작은 오차가 존재하게 되기 때문이다. 이것은 자바뿐만 아니라 모든 프로그램이 언어에서 발생하는 기본적인 문제다.

다음으로 실수를 부동 소수점으로 변환하는 방법에 대해 알아보자.

실수의 부동 소수점 변환

정수부는 10진수에 2를 나눠가며 구하고 소수부는 10진수에 2를 곱해가며 구한다. 0.625를 2진수로 변환하는 과정을 살펴보자.

0.625 x 2 = 1.25 → 1을 빼내고 나머지 0.25
0.25 x 2 = 0.5 → 0을 빼내고 나머지 0.5
0.5 x 2 = 1 → 1을 빼내고 나머지 0

이제 나머지가 0이 나왔으니 변환을 종료하고 빼낸 숫자를 위에서부터 읽어주면 된다.

즉 0.625 → 0.101₍₂₎이 된다.

0.5, 0.25, 0.125, 0.75와 같은 숫자들이 2진수로 변환하기 편하고, 반대로 0.789와 같은 숫자는 10진수 기준으로는 자릿수가 길지 않더라도 2진수로 바꾸면 엄청나게 길이가 늘어난다.

저작자표시 비영리 변경금지

'CS' 카테고리의 다른 글

DAO, DTO, VO, ENTITY (1)	2023.09.03
[CS] 슬라이싱 (0)	2023.04.12
[CS] 라이브러리(library) (0)	2023.04.06