
이진 탐색 - 자료구조와 알고리즘
탐색 알고리즘 중 하나인 이진 탐색(Binary Search)이란 '정렬된 배열'에서 '특정 값'을 찾는 알고리즘을 의미한다. 이진 검색은 정렬된 배열에서 검색 간격을 반으로 반복적으로 나누어 사용하는 검색 알고리즘으로 정의된다. 이진 검색의 아이디어는 배열이 정렬된 정보를 사용하여 시간 복잡도를 O(로그 N)으로 줄이는 것이다.
이진 탐색 알고리즘의 예시로 아래의 그림을 참고하자.

정렬된 배열에서 23을 찾는 과정이다.
- 배열의 중앙 인덱스를 찾는다.
M = (0 + 9) / 2 = 4 - 인덱스 4에 위치한 16과 23을 비교한다.
16 < 23 - 23이 더 크므로 L(5) ~ H(9) 사이에서 다시 탐색을 실시한다.
M = (5 + 9) / 2 = 7 - 인덱스 7에 위치한 56과 23을 비교한다.
56 > 23 - 23이 더 작으므로 L(5) ~ H(7) 사이에서 다시 탐색을 실시한다.
M = (5 + 7) / 2 = 6 - 인덱스 6에 위치한 38과 23을 비교한다.
38 > 23 - 38이 더 크므로 L(5) ~ H(6) 사이에서 탐색을 실시한다.
M = (5 + 6) / 2 = 5 - 23을 찾았고, 인덱스 5를 반환한다.
위와 같은 과정을 거쳐서 탐색을 진행한다.
1. 자료구조는 반드시 정렬되어 있어야 한다.
2. 자료구조의 어떤 요소에 접근하는 시간은 상수여야 한다.
그림과 함께 이분 탐색 알고리즘을 살펴보자.
이진 탐색 알고리즘
이진 탐색 알고리즘은 중간 인덱스인 mid를 찾아 검색 공간을 두 개의 절반으로 나눈다.

- 검색 공간의 중간 요소를 키와 비교한다.
- 중간 요소에서 키를 찾으면 프로세스가 종료된다.
- 중간 요소에서 키를 찾지 못하면 다음 검색 공간으로 사용할 절반을 선택한다.
- 키가 중간 요소보다 작으면 왼쪽이 다음 검색에 사용된다.
- 키가 중간 요소보다 크면 오른쪽이 다음 검색에 사용된다.
- 이 과정은 키를 찾거나 전체 검색 공간이 모두 소진될 때까지 계속된다.
이진 탐색은 어떻게 동작할까?
배열 arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}이고 대상 = 23이라고 가정해보자.
첫 번째 단계
mid을 계산하고 arr[mid]와 key를 비교한다. key가 arr[mid]보다 작으면 왼쪽으로 이동하고, arr[mid]보다 크면 검색 공간을 오른쪽으로 이동한다. key(23)가 현재 arr[mid](16)보다 크다. 검색 공간이 오른쪽으로 이동한다.

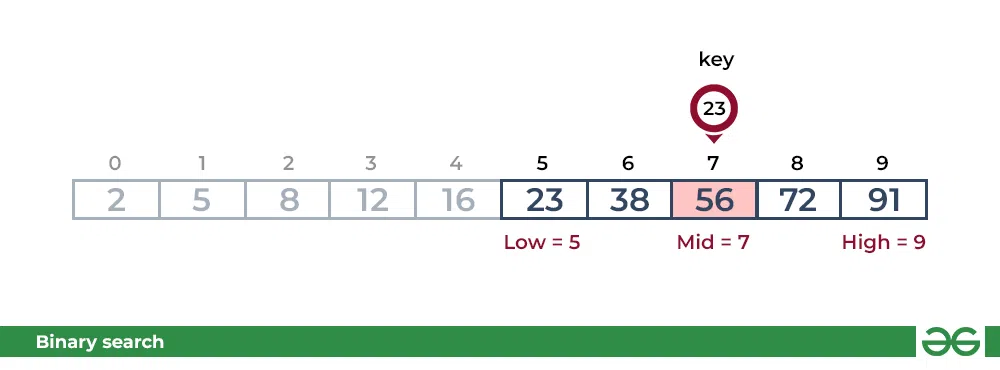
두번째 단계
key가 arr[mid]의 값과 일치하면 해당 요소를 찾은 것으로 간주하고 검색을 중지한다.

이진 탐색은 어떻게 구현할까?
이진 탐색은 두 가지 방법으로 구현할 수 있다.
- 반복 이진 탐색 알고리즘
- 재귀 이진 탐색 알고리즘
반복 이진 검색 알고리즘부터 알아보자.
반복 이진 탐색 알고리즘
여기서는 while 루프를 사용하여 키를 비교하고 검색 공간을 두 개로 분할하는 프로세스를 계속 진행한다.
코드를 통해 살펴보자.
// Java implementation of iterative Binary Search
import java.io.*;
class BinarySearch {
// Returns index of x if it is present in arr[].
int binarySearch(int arr[], int x)
{
int l = 0, r = arr.length - 1;
while (l <= r) {
int m = l + (r - l) / 2;
// Check if x is present at mid
if (arr[m] == x)
return m;
// If x greater, ignore left half
if (arr[m] < x)
l = m + 1;
// If x is smaller, ignore right half
else
r = m - 1;
}
// If we reach here, then element was
// not present
return -1;
}
// Driver code
public static void main(String args[])
{
BinarySearch ob = new BinarySearch();
int arr[] = { 2, 3, 4, 10, 40 };
int n = arr.length;
int x = 10;
int result = ob.binarySearch(arr, x);
if (result == -1)
System.out.println(
"Element is not present in array");
else
System.out.println("Element is present at "
+ "index " + result);
}
}
위의 코드를 실행시켰을 때 아래와 같은 결과를 얻을 수 있다.
Element is present at index 3
위 코드의 시간 복잡도와 공간 복잡도를 분석하면 아래와 같다.
시간 복잡도: O(logN)
보조 공간 복잡도: O(1)
재귀 이진 탐색 알고리즘
재귀 함수를 만들어 검색 공간의 중간을 키와 비교한다. 그리고 그 결과에 따라 키가 발견된 인덱스를 반환하거나 다음 검색 공간에 대한 재귀 함수를 호출한다. 이 방법 또한 아래 코드를 통해 살펴보자.
// Java implementation of recursive Binary Search
class BinarySearch {
// Returns index of x if it is present in arr[l..
// r], else return -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l) {
int mid = l + (r - l) / 2;
// If the element is present at the
// middle itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then
// it can only be present in left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid - 1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid + 1, r, x);
}
// We reach here when element is not present
// in array
return -1;
}
// Driver code
public static void main(String args[])
{
BinarySearch ob = new BinarySearch();
int arr[] = { 2, 3, 4, 10, 40 };
int n = arr.length;
int x = 10;
int result = ob.binarySearch(arr, 0, n - 1, x);
if (result == -1)
System.out.println(
"Element is not present in array");
else
System.out.println(
"Element is present at index " + result);
}
}
/* This code is contributed by Rajat Mishra */
위 코드를 실행하면 이전과 마찬가지로 똑같은 결과를 얻게 된다.
Element is present at index 3
위 코드의 시간 복잡도와 공간 복잡도를 분석하면 아래와 같다.
시간 복잡도:
- 최고: O(1)
- 평균: O(logN)
- 최악: O(logN)
보조 공간 복잡도: O(1)이나 재귀 호출 스택을 고려하면 보조 공간은 O(logN)이 된다.
이진 탐색 정리
이진 검색의 장점
- 이진 탐색은 특히 큰 배열에 대해서 선형 탐색보다 빠르다.
- 다른 시간 복잡도를 가진 탐색 알고리즘들(예: 보간 탐색 또는 지수 탐색)에 비해 더 효율적이다.
- 이진 탐색은 하드 드라이브나 클라우드와 같은 외부 메모리에 저장된 대량의 데이터셋을 검색하는 데 적합하다.
이진 탐색의 단점
- 배열은 정렬되어 있어야 한다.
- 이진 탐색은 검색 대상인 데이터 구조가 연속된 메모리 위치에 저장되어 있어야 한다.
- 이진 탐색은 배열의 요소들이 비교 가능해야 한다.
이진 탐색의 응용
- 이진 탐색은 기계 학습에서 더 복잡한 알고리즘의 구성 요소로 사용될 수 있다. 예를 들어, 신경망을 훈련하거나 모델의 최적 하이퍼파라미터를 찾는 알고리즘에 사용될 수 있다.
- 컴퓨터 그래픽스에서 레이 트레이싱이나 텍스처 매핑과 같은 알고리즘에서 검색에 사용될 수 있다.
- 데이터베이스 검색에 활용될 수 있다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 우선순위 큐(Priority Queue) (0) | 2023.09.05 |
|---|---|
| [백준 2338 자바/Java] 긴자리 계산 (0) | 2023.05.23 |
| [백준 2309 파이썬/python] 일곱 난쟁이 (1) | 2023.05.17 |
| [백준 10812 파이썬/python] 바구니 순서 바꾸기 (0) | 2023.05.17 |
| [백준 17404 파이썬/python] RGB거리 2 (0) | 2023.05.17 |
