백준에서 알고리즘 문제를 풀고, 다른 사람들의 풀이를 보다가 우선순위 큐를 사용하여 문제를 푼 풀이를 보고 우선순위 큐가 어떤 자료구조인지 공부하기 위해 오늘 글을 포스팅한다.
1. 스택(Stack)
- 데이터를 선형으로 저장하는 자료구조.
- 후입선출(LIFO)
- 가장 최근에 추가된 항목이 가장 먼저 제거 → 주로 함수 호출(Call Back)을 구현하거나 역추적(Backtracking) 알고리즘에 사용
- 주요 연산은 Push와 Pop
2. 큐(Queue)
- 데이터를 선형으로 저장하는 자료구조.
- 선입선출(FIFO)
- 가장 먼저 추가된 항목이 가장 먼저 제거 → 대기열이나 작업 스케줄링(Task Scheduling)과 같이 순서가 중요한 상황에 사용
- 주요 연산은 enqueue(), dequeue()
- enqueue(): 항목에 큐를 추가하는 작업
- dequeue(): 가장 앞에 있는 항목을 제거하고 반환하는 작업
3. 우선순위 큐(Priority Queue)
1) 설명
- 먼저 들어온 순서대로 데이터가 나가는 것이 아닌 우선순위를 먼저 결정하고 그 우선순위가 높은 엘리먼트가 먼저 나가는 자료구조
- 힙을 이용하여 구현하는 것이 일반적
- 진행방식
- 데이터 삽입 시 우선순위를 기준으로 최대 힙 혹은 최소 힙을 구성
- 데이터를 꺼낼 때 루트 노드를 얻어냄
- 루트 노드를 삭제 시 빈 루트 노드 위치에 맨 마지막 노드를 삽입
- 그 후 아래로 내려가면서 적절한 자리를 찾아서 옮긴다.
2) 특징
- 모든 항목에는 우선순위가 있음
- 높은 우선순위의 요소를 먼저 꺼내서 처리하는 구조(큐에 들어있는 원소가 비교 가능한 수준이어야 함)
- 내부 요소는 힙으로 구성되어 이진트리 구조로 이루어져 있음
- 내부구조가 힙으로 구성되어 있기에 시간 복잡도는 O(NlogN)
- 응급실과 같이 우선순위를 중요시해야 하는 상황에 쓰인다.

9 → 6 → 7 → 1 → 8 순으로 데이터가 들어간다고 가정했을 때 우선순위 큐의 처리 순서는 다음과 같다.
(높은 값이 높은 우선순위를 갖는다고 가정)
- Input: 9 → 6 → 7 → 1 → 8
- Queue: 9 → 6 → 7 → 1 → 8
- Priority Queue: 9 → 8 → 7 → 6 → 1
3) 주요 연산
- enqueue(): queue에 새로운 요소 삽입
- dequeue(): queue에서 최대 우선 순위 요소를 삭제하고 그 값을 반환
- peek(): queue에서 최대 우선순위 요소를 반환
4) 구현
큐 구현 방식에는 배열, 연결 리스트, 힙이 있음
시간 복잡도
| 구현 방법 | enqueue() | dequeue() |
| 배열 (unsorted array) | O(1) | O(N) |
| 연결 리스트 (unsorted linked list) | O(1) | O(N) |
| 정렬된 배열 (sorted array) | O(N) | O(1) |
| 정렬된 연결 리스트 (sorted linked list) | O(N) | O(1) |
| 힙 (heap) | O(logN) | O(logN) |
힙 방식이 최악의 경우라도 O(logN)을 보장하기에 일반적으로 힙으로 구현한다.
우선순위 큐 요소의 구조
struct node {
int data;
int priority;
}가정
- 배열에는 우선순위만 들어있다.
- 값이 클수록 우선순위가 높다. (최대 힙)
- size 변수는 전역변수, 힙에 존재하는 요소 수를 나타냄
- 루트 노드는 index 1에 위치함
1. peek()
최대 우선순위 값(최대 힙)은 항상 루트에 있으므로 루트 값 반환
int peek(int arr[]) {
return arr[i];
}시간 복잡도: O(1)
2. enqueue()
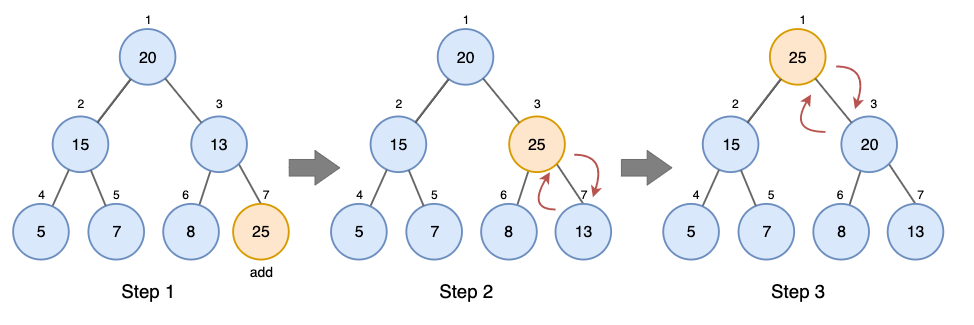
우선순위 큐(최대 힙)에 요소를 삽입하는 작업
- 힙 끝에 새로운 요소 삽입
- 부모 노드와 비교하여 힙 속성을 위배하는 경우 부모 노드와 값 변경
- 힙 속성이 유지될 때까지 2번 작업 반복
void enqueue(int arr[], int val)
{
int i = 0;
if (size == MAX_LEN) { // 배열에 공간이 없으면 실패
printf("Overflow: Could not insertKey\n");
}
// 힙 끝에 요소 삽입.
size ++;
i = size;
arr[i]= val;
// 우선순위가 부모 노드가 더 작다면 교환하고 부모 노드부터 다시 비교, 힙속성을 유지할 때까지 반복함.
while(i > 1 && arr[i/2] < arr[i]) {
swap(arr[i/2], arr[i]);
i = i/2;
}
}시간복잡도: O(logN)
3. heapify()
힙 속성을 유지하는 작업. 위에서 아래로(Top-Bottom). 최대 힙에서 heapify의 작업 과정은 아래와 같다.
- 자식 노드와 우선순위 비교
- 자식 노드 우선순위가 높다면 왼쪽, 오른쪽 자식 중 가장 우선순위가 높은 노드와 교환
- 힙 속성이 유지 될 때까지 1, 2번 과정 반복

void max_heapify (int arr[], int i)
{
int largest = i;
int left = 2*i //left child
int right = 2*i +1 //right child
// 현재 요소 i와 자식 노드의 값을 비교
if(left <= size && arr[left] > arr[i] )
largest = left;
if(right <= size && arr[right] > arr[largest] )
largest = right;
// 자식 노드의 값이 더 크다면 교환하고 교환된 자식 노드부터 heapify 진행
if(largest != i ) {
swap (arr[i] , arr[largest]);
max_heapify (h, largest);
}
}시간복잡도: O(logN)
4. dequeue()
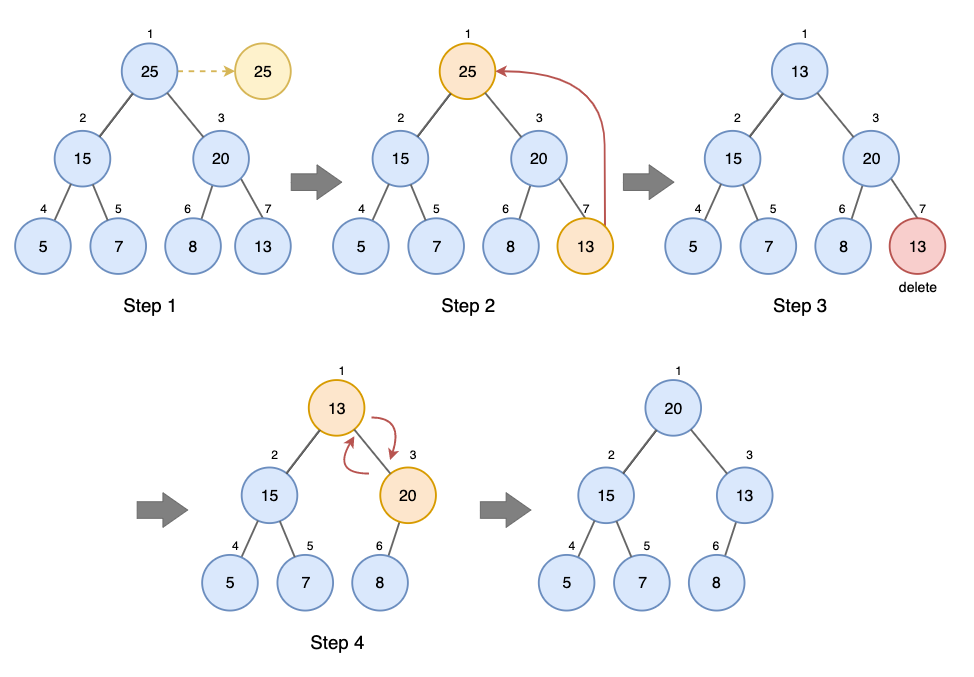
우선 순위 큐(최대 힙)에 최대 우선순위 요소를 삭제하고 그 값을 반환하는 작업
- 루트 노드의 값을 추출
- heap 마지막 요소를 루트 노드에 배치
- 마지막 요소는 제거
- 루트 노드부터 heapify 수행
int dequeue (int arr[]) {
if(size == 0) {
printf("empty\n");
}
// 루트 노드 값을 리턴값에 저장한 뒤, 마지막 요소를 루트노드에 배치함
Node max = arr[1];
arr[1] = arr[size];
size --;
// 루트 노드부터 heapify 수행
max_heapify(arr, 1);
return max;
}5) 사용 사례
CPU 스케줄링, 다익스트라 최단경로 알고리즘, Prim의 MST(Minimum Spanning Tree) 알고리즘, 우선순위를 포함한 모든 queue의 응용에 사용된다.
참고자료
[자료구조] 우선순위 큐 (Priority Queue) 개념 및 구현 (tistory.com)
[자료구조] 우선순위 큐 (Priority Queue) 개념 및 구현
목차 우선순위 큐 (Priority Queue) 개념 및 구현 일반적인 큐(Queue)는 먼저 집어넣은 데이터가 먼저 나오는 FIFO (First In First Out) 구조로 저장하는 선형 자료구조입니다. 하지만 우선순위 큐(Priority Queue
yoongrammer.tistory.com
[Java] PriorityQueue(우선순위 큐) 클래스 사용법 & 예제 총정리 (tistory.com)
[Java] PriorityQueue(우선순위 큐) 클래스 사용법 & 예제 총정리
우선순위 큐(Priority Queue)란? 일반적으로 큐는 데이터를 일시적으로 쌓아두기 위한 자료구조로 스택과는 다르게 FIFO(First In First Out)의 구조 즉 먼저 들어온 데이터가 먼저 나가는 구조를 가집니다
coding-factory.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] Binary Search (1) | 2024.01.30 |
|---|---|
| [백준 2338 자바/Java] 긴자리 계산 (0) | 2023.05.23 |
| [백준 2309 파이썬/python] 일곱 난쟁이 (1) | 2023.05.17 |
| [백준 10812 파이썬/python] 바구니 순서 바꾸기 (0) | 2023.05.17 |
| [백준 17404 파이썬/python] RGB거리 2 (0) | 2023.05.17 |