반응형
1. 2. 구간합
- 구간 합은 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘. 코딩 테스트에서 사용 빈도 높음!
1.1. 구간 합의 핵심 이론
1.1.1. 합 배열 S 정의
<code />
S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i] // A[0]부터 A[i]까지의 합
합 배열은 기존의 배열을 전처리한 배열.
합 배열을 미리 구해두면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소!

A[i]부터 A[j]까지의 배열 합을 합 배열 없이 구하는 경우, 최악의 경우는 i가 0이고 j가 N인 경우로 시간 복잡도는 O(N)이다.
합 배열을 사용한다면 O(1) 안에 답을 구할 수 있다.
1.1.2. 합 배열 S를 만드는 공식
<code />
S[i] = S[i - 1] + A[i]
1.1.3. 구간 합을 구하는 공식
<code />
S[j] - S[i - 1] // i에서 j까지 구간 합

1.1.4. A[2] ~ A[5] 구간 합을 합 배열로 구하는 과정
<code />
S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] = A[2] + A[3] + A[4] + A[5]
1.2. [⭕️][백준 11659] 구간 합 구하기

1.2.1. 1단계 - 문제 분석하기
- 수의 개수와 합을 구해야 하는 횟수는 최대 100,000 → 구간마다 합을 매번 계산하면 0.5초 안에 모든 구간 합 계산 불가
- 구간 합을 매번 계산하면? 최악의 경우 100,000 * 1,000 = 100,000,000 → 최악의 경우 1억 회 이상의 연산을 수행하게 되어 1초 이상의 수행 시간 필요!
1.2.2. 2단계 - 손으로 풀어 보기
- 합 배열 공식
S[i] = S[i-1] + A[i]

- 구간 합 공식
S[j] - S[i-1]
<code />
질의1(1, 3): S[3] - S[0] = 12 0 = 12
질의2(2, 4): S[4] - S[1] = 14 5 = 9
질의3(5, 5): S[5] - S[4] = 15 14 = 1
1.2.3. 3단계 - 슈도코드 작성하기
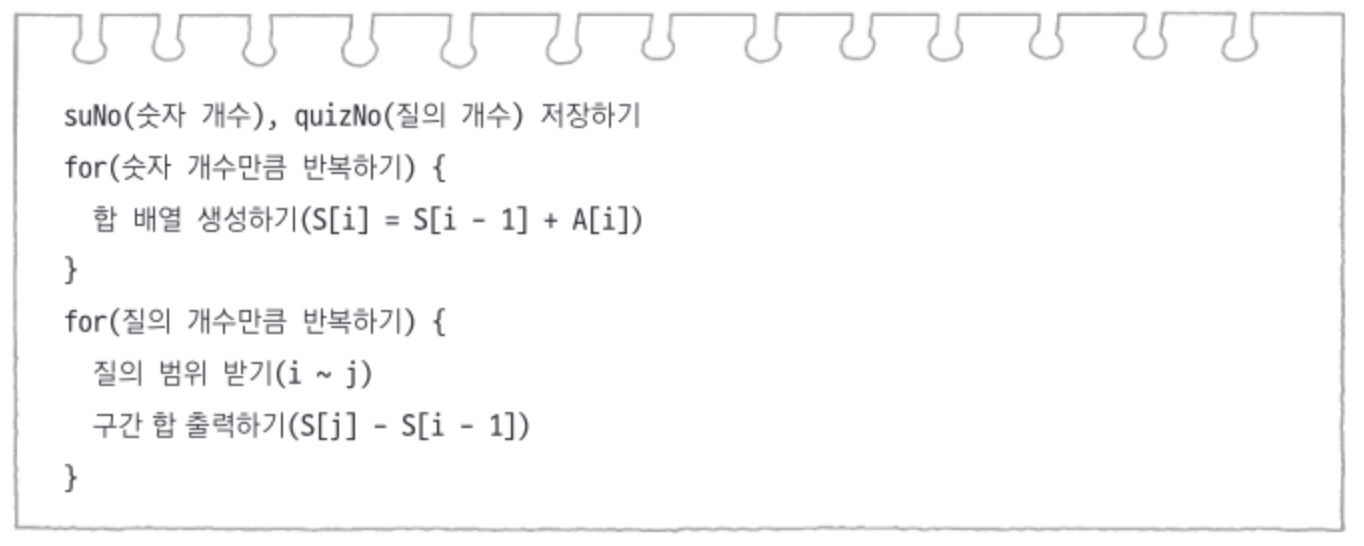
1.2.4. 4단계 - 코드 구현하기
<code />
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 숫자 갯수
int m = Integer.parseInt(st.nextToken()); // 질의 갯수
long[] S = new long[n + 1]; // 구간합 배열 선언
st = new StringTokenizer(br.readLine());
for (int i = 1 ; i <= n ; i++) {
S[i] = S[i - 1] + Integer.parseInt(st.nextToken());
}
for (int q = 0 ; q < m ; q++) {
st = new StringTokenizer(br.readLine());
int i = Integer.parseInt(st.nextToken());
int j = Integer.parseInt(st.nextToken());
System.out.println(S[j] - S[i - 1]);
}
}
}
1.3. [⚠️][백준 11660] 구간 합 구하기 5

1.3.1. 1단계 - 문제 분석하기
- 횟수 M이 100,000개 → 질의마다 합을 구하는 것이 아닌 구간 합 배열을 이용해야함.
- 2차원 구간 합 배열 D[X][Y] 정의
<code />
D[X][Y] = 원본 배열의 (0, 0)부터 (X, Y)까지의 사각형 영역 안에 있는 수의 합
1.3.2. 2단계 - 손으로 풀어 보기
- 2차원 구간 합 배열의 1행, 1열부터 구한다. 구간 합 배열 1행, 1열은 다음과 같다.
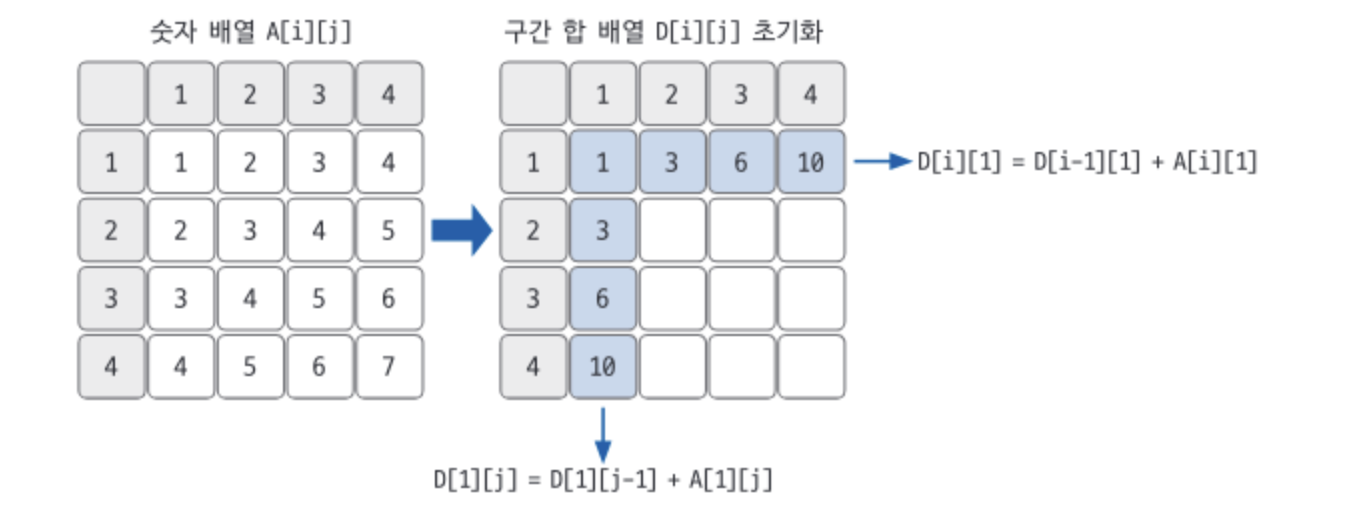
- 이를 통해 나머지 2차원 구간 합 배열을 채운다.
- D[i][j]의 값을 채우는 구간 합 공식
<code />
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]

- 구간 합 배열을 이용하기 전에 질의에 대한 답을 도출하기 위한 과정을 원본 배열과 함께 살펴봄.
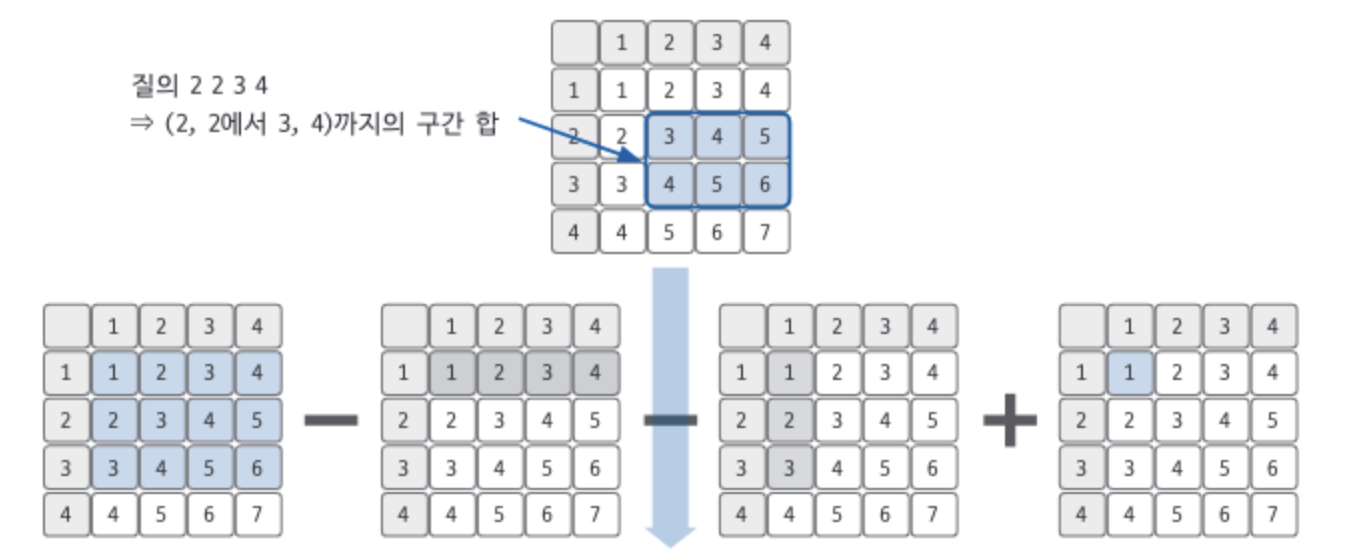
예를 들어 질의가 2 2 3 4라면 (3,4) 구간 합에서 (1,4) 구간 합, (3,1) 구간 합을 뺀 다음, 중복하여 뺀 (1,1) 구간 합을 더하면 된다.
원본 배열에 표시한 구간 합을 다시 구간 합 배열에 표시하면 다음과 같다.

<code />
→ D[3][4] - D[1][4] - D[3][1] + D[1][1] = 27
- 질의에 대한 답을 구하는 공식
<code />
D[X2][Y2] - D[X1 - 1][Y2] - D[X2][Y1-1] + D[X1-1][Y1-1]
1.3.3. 3단계 - 슈도코드 작성하기

1.3.4. 4단계 - 코드 구현하기
- 정답코드
<code />
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 표의 크기
int m = Integer.parseInt(st.nextToken()); // 질의 갯수
int A[][] = new int[n + 1][n + 1];
for (int i = 1 ; i <= n ; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1 ; j <= n ; j++) {
A[i][j] = Integer.parseInt(st.nextToken());
}
}
int D[][] = new int[n + 1][n + 1];
for (int i = 1 ; i <= n ; i++) {
for (int j = 1 ; j <= n ; j++) {
// 구간 합 구하기
D[i][j] = D[i][j - 1] + D[i - 1][j] - D[i - 1][j - 1] + A[i][j];
}
}
for (int i = 0 ; i < m ; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 구간 합 배열로 질의에 답변
int result = D[x2][y2] - D[x2][y1 - 1] - D[x1 - 1][y2] + D[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}
- 내 코드
<code />
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 첫째줄 - 표의 크기 n, 합을 구해야 하는 횟수 m
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
// 둘째줄부터 n개의 줄
int arr[][] = new int[n + 1][n + 1];
for (int i = 1 ; i <= n ; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1 ; j <= n ; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
// 구간 합 구하기
int arrSum[][] = new int[n + 1][n + 1];
// 빈 배열값은 0으로 채워진다!!
// arrSum[1][1] = arr[1][1];
// for (int i = 2 ; i <= n ; i++) {
// arrSum[1][i] = arrSum[1][i - 1] + arr[1][i];
// }
// for (int i = 2 ; i <= n ; i++) {
// arrSum[i][1] = arrSum[i-1][1] + arr[i][1];
// }
for (int i = 1 ; i <= n ; i++) {
for (int j = 1 ; j <= n ; j++) {
arrSum[i][j] = arrSum[i-1][j] + arrSum[i][j-1] + arr[i][j] - arrSum[i-1][j-1];
}
}
// m번 만큼 질의에 대한 값 출력
for (int i = 0 ; i < m ; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
System.out.println(arrSum[x2][y2] - arrSum[x2][y1 - 1] - arrSum[x1 - 1][y2] + arrSum[x1 - 1][y1 - 1]);
}
}
}
1.4. [❌][백준 10986] 나머지 합 구하기

1.4.1. 1단계 - 문제 분석하기
- N의 최댓값이 106이라 연산량이 작게 느껴질 수도 있으나 106개의 수에 대하여 모든 구간 합을 구해야 하므로 1초 안에 연산하기 어려움
→ 여기서도 구간 합 배열을 이용해야 한다. - 나머지 합 문제 풀이의 핵심 아이디어
- (A + B) % C은 ((A % C) + (B % C)) % C와 같다.
→ 특정 구간 수들의 나머지 연산을 더해 나머지 연산을 한 값과 이 구간 합의 나머지 연산을 한 값은 동일하다. - 구간 합 배열을 이용한 식 S[i] - S[j]는 원본 배열의 j + 1부터 i까지의 구간 합이다.
- S[i] % M의 값과 S[j] % M의 값이 같다면 (S[i] - S[j]) % M은 0이다.
→ 구간 합 배열의 원소를 M으로 나눈 나머지로 업데이트하고 S[i]와 S[j]가 같은 (i,j)쌍을 찾으면 원본 배열에서 j + 1부터 i까지의 구간 합이 M으로 나누어 떨어진다!!
- (A + B) % C은 ((A % C) + (B % C)) % C와 같다.
1.4.2. 2단계 - 손으로 풀어 보기
- A 배열의 합 배열 S를 생성

- 합 배열 S의 모든 값을 M으로 나머지 연산을 수행해 값을 업데이트

- 우선 변경된 합 배열에서 원소 값이 0인 개수만 세어 정답에 더한다.
변경된 합 배열의 원소 값이 0이라는 뜻은 원본 배열의 0부터 i까지의 구간 합이 이미 M으로 나누어 떨어진다는 뜻이기 때문 - 경우의 수 = +3
- 변경된 합 배열에서 원소 값이 같은 인덱스의 개수 → 나머지 값이 같은 합 배열의 개수를 센다.
변경된 합 배열에서 원소 값이 같은 2개의 원소를 뽑는 모든 경우의 수를 구하여 정답에 더하면 된다.
위의 예에서는 0이 3개, 1이 2개이므로 ₃C₂, ₂C₂로 경우의 수를 구하여 더하면 된다.- ₃C₂ = 3 → 경우의 수 = + 3
- ₂C₂ = 1 → 경우의 수 = + 1
- 총 경우의 수 = 3 + 3 + 1 = 7
1.4.3. 3단계 - 슈도코드 작성하기

1.4.4. 4단계 - 코드 구현하기
<code />
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
long S[] = new long[N];
long C[] = new long[M];
long answer = 0;
st = new StringTokenizer(br.readLine());
S[0] = Integer.parseInt(st.nextToken());
for(int i = 1; i < N; i++) {
S[i] = S[i-1] + Integer.parseInt(st.nextToken());
}
for(int i = 0; i < N; i++) {
int remainder = (int)(S[i] % M);
if (remainder == 0) {
answer++;
}
C[remainder]++;
}
for(int i = 0; i < M; i++) {
if (C[i] > 1) {
answer += (C[i] * (C[i] - 1) / 2);
}
}
System.out.println(answer);
}
}반응형
'TIL' 카테고리의 다른 글
| [TIL-18 / 230907] 함수형 프로그래밍, 컬렉션 프레임워크 (0) | 2023.09.08 |
|---|---|
| [TIL-17 / 230710] 알고리즘 - 슬라이딩 윈도우(백준 12891) (1) | 2023.07.10 |
| [TIL-15 / 230705] 알고리즘 - 배열과 리스트 (0) | 2023.07.06 |
| [TIL-14 / 230702] 알고리즘 - 카운팅 정렬(Counting Sort) (0) | 2023.07.02 |
| [TIL-13 / 230701] 알고리즘 - 디버깅 (0) | 2023.07.01 |

