4. 기본형(primitive type)
4.1 논리형 - boolean
- true / false
4.2 문자형 - char
- 단 하나의 문자만을 저장할 수 있음, 문자가 저장되는 것이 아닌 ‘문자의 유니코드(정수)’가 저장됨.
char ch = 'A'; // 문자 'A'를 char 타입의 변수로 ch에 저장. A의 유니코드 값인 65가 저장됨.
char ch = 65; // 문자의 코드를 직접 변수 ch에 저장
int code = (int)ch; // ch에 저장된 값을 int 타입으로 변환하여 저장한다 -> 형변환(캐스팅,casting)
- 특수문자를 표현하는 방법
|
특수문자
|
문자 리터럴
|
|
tab
|
\t
|
|
backspace
|
\b
|
|
form feed
|
\f
|
|
new line
|
\n
|
|
carriage return
|
\r
|
|
역슬래쉬(\)
|
\\
|
|
작은 따옴표
|
\’
|
|
큰 따옴표
|
\”
|
|
유니코드(16진수) 문자
|
\u유니코드(ex. char a = ‘\u0041’)
|
- 인코딩과 디코딩(encoding & decoding)
4.1.1 아스키(ASCII; American Standard Code for Information Interchange)
- 의미 : 정보 교환을 위한 미국 표준 코드
- 내용 : 128개(=2⁷)의 문자 집합(character set)을 제공하는 7 bit 부호, 처음 32개의 문자는 인쇄와 전송 제어용으로 사용되는 제어문자(control character)로 출력할 수 없고 마지막 문자(DEL)를 제외한 33번째 이후의 문자들은 출력할 수 있는 문자들로 기호와 숫자, 영대소문자로 이루어짐.
- 특징 : 숫자(0~9), 영문자(A~Z, a~z)가 연속적으로 배치되어 있다는 특징
4.1.2 확장 아스키(Extended ASCII)와 한글
- 일반적으로 데이터는 byte 단위로 다뤄지는데 아스키는 7 bit 이므로 1 bit 가 남는다. 이 남는 공간을 활용해서 문자를 추가로 정의한 것이 ‘확장 아스키’ 이다.
- ISO(국제표준화기구)에서 발표한 확장 아스키의 표준 중에 대표적인 것이 ‘ISO 8859-1’이다. 이 확장 아스키 버젼은 ‘ISO Latin 1’ 이라고도 하는데 서유럽에서 일반적으로 사용하는 문자들을 포함하고 있다.
- 한글을 표현하는 방법 - 두 개의 문자코드로 한글을 표현함
- 유니코드(Unicode)
- 유니코드 인코딩 UTF-8과 UTF-16의 비교
4.3 정수형 - byte(1) < short(2) < int(4) < long(8)
4.3.1 정수형의 선택기준
- byte 나 short 보다 int를 사용하라. (int의 표현가능한 정수 범위 ±20억)
4.3.2 정수형의 오버플로우(overflow)
ex) 자동차 주행 표시기(odometer), 계수기(counter)
|
|
1
|
1
|
1
|
1
|
|
+
|
0
|
0
|
0
|
1
|
|
|
?
|
?
|
?
|
?
|
- 원래 2진수 ‘1111’ 에 1 을 더하면 ‘10000’ 이 되지만, 4 bit 로는 4자리의 2진수만 저장할 수 있기 때문에 ‘0000’이 됨. 즉 5자리의 2진수 ‘10000’ 중에서 하위 4 bit 만 저장하게 되는 것.
- 예시
public class OverflowEx {
public static void main(String[] args) {
short sMin = -32768;
short sMax = 32767;
char cMin = 0;
char cMax = 65535;
System.out.println("sMin = " + sMin);
System.out.println("sMin - 1 = " + (short)(sMin-1));
System.out.println("sMax = " + sMax);
System.out.println("sMax + 1 = " + (short)(sMax+1));
System.out.println("cMin = " + (int)cMin);
System.out.println("cMin - 1 = " + (int)--cMin);
System.out.println("cMax = " + (int)cMax);
System.out.println("cMax + 1 = " + (int)++cMax);
}
}// 실행결과
sMin = -32768
sMin - 1 = 32767
sMax = 32767
sMax + 1 = -32768
cMin = 0
cMin - 1 = 65535
cMax = 65535
cMax + 1 = 0
4.4 실수형 - float, double
4.4.1 실수형의 범위와 정밀도
|
타입
|
저장 가능한 값의 범위
|
정밀도
|
크기 - byte(bit)
|
|
float
|
-3.4 x 10³⁸ ~ -1.4 x 10⁻⁴⁵, 1.4 x 10⁻⁴⁵ ~ 3.4 x 10³⁸
|
7자리
|
4(32)
|
|
double
|
-1.8 x 10³⁰⁸ ~ 4.9 x 10^³²⁴, 4.9 x 10⁻³²⁴ ~ 1.8 x 10³⁰⁸
|
15자리
|
8(64)
|
4.4.2 실수형의 오버플로우와 언더플로우
- 오버플로우 : 표현범위의 최대값을 벗어났을 때 발생. 실수형에서는 무한대(infinity)가 됨.
- 언더플로우 : 실수형으로 표현할 수 없는 아주 작은 값, 양의 최소값보다 작은 값이 되는 경우. 이때 변수의 값은 0이 됨.
4.4.3 같은 4 byte 로 int 보다 훨씬 큰 값을 표현할 수 있는 이유?
→ 값을 저장하는 형식이 다르기 때문!
- int 타입과 float 타입의 표현 형식
- float 타입과 같은 실수형은 부호(S), 지수(E), 가수(M) 세 부분으로 이루어져 있다.
- 그러나 정수형과 달리 실수형은 오차가 발생할 수도 있다는 단점 존재
4.4.4 실수형의 저장형식
|
기호
|
의미
|
설명
|
|
S
|
부호(Sign bit)
|
0이면 양수, 1이면 음수
|
|
E
|
지수(Exponent)
|
부호있는 정수. 지수의 범위 : -127 ~ 128(float), -1023 ~ 1024(double)
|
|
M
|
가수(Mantissa)
|
실제값을 저장하는 부분. 정밀도 : 10진수로 7자리(float), 15자리(double)
|
- 부호(Sign bit)
- 지수(Exponent)
- 가수(Mantissa)
4.4.5[⭐︎⭐︎⭐︎] 정규화
- 부동 소수점 오차의 발생 이유
ex. 1001.000111111001101011011011… →(정규화)→ 1.001000111111001101011011011... X 2³
⎣____ 23 bit ____⎦
정규화된 2진 실수는 항상 ‘1.’으로 시작하기에 ‘1.’을 제외한 23자리의 2진수가 가수(mantissa)로 저장되고 그 이후는 잘려나간다. 지수는 기저법으로 저장되기 때문에 지수인 3에 기저인 127을 더한 130이 2진수로 변환되어 저장된다. 10진수 130은 2진수로 ‘10000010’이다.
이 때 잘려나간 값들에 의해 발생할 수 있는 최대오차는 약 2⁻²³인데, 이 값은 가수의 마지막 비트의 단위와 같음.
2⁻²³은 10진수로 0.0000001192(약 10⁻⁷)이므로 float의 정밀도가 7자리(소수점 이하 6자리)라고 한다.
- [예제] 9.1234567을 floatToBits() 메서드를 이용하여 16진수로 출력하라.
☆한번에 이해하기 어려운 개념! <보충 설명>

- 10진수를 2진수로 변환 그리고 정규화 과정 : 7.625 → 111.101₍₂₎ →(정규화)→ 1.11101 x 2²
- 부호비트 : 0(양수), 1(음수)
- 가수부(23자리) : 정규화 결과 소수점 오른쪽에 있는 숫자들을 왼쪽부터 그대로 넣고 남은 자리는 0으로 채움.
(소수점 왼쪽은 정규화를 하면 무조건 1이기 때문에 신경쓰지 않고 표현도 하지 않음. 이 1을 hidden bit이라 함)
- 지수부(8자리) : 2ⁿ에서 n에 해당하는 수인 2를 2진수로 바꾼 10’을 넣으면 될 것 같다.

- bias 값을 쓰는 이유?
- 이와 같이 부동 소수점 표현 방식은 고정 소수점 표현 방식에 비해서 비트 수 대비 표현 가능한 수의 범위와 정밀도 측면에서 우위에 있기 때문에 정규화나 bias와 같은 복잡한 과정이 들어가더라도 대부분 컴퓨터 시스템에서 부동 소수점을 이용해 실수를 표현하고 있다.
4.4.6 실수 표현 방식의 종류
- 가수부와 지수부
- 고정 소수점 (fixed point) 방식

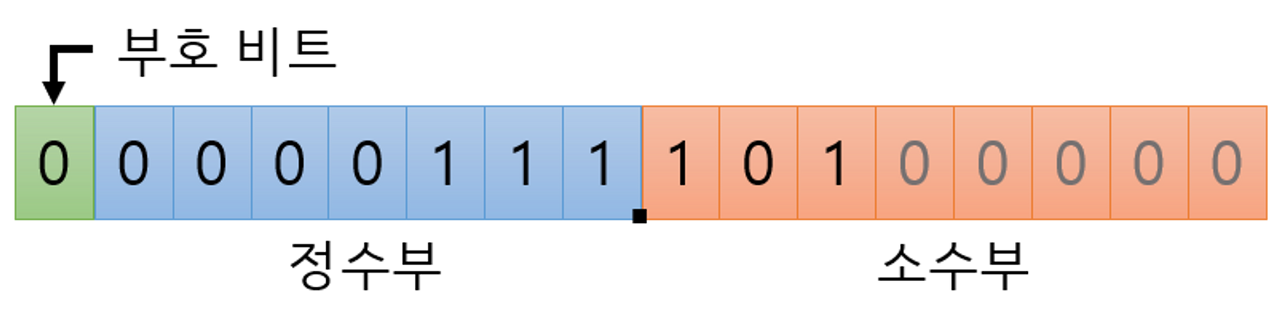
- 부동 소수점(floating point) 방식
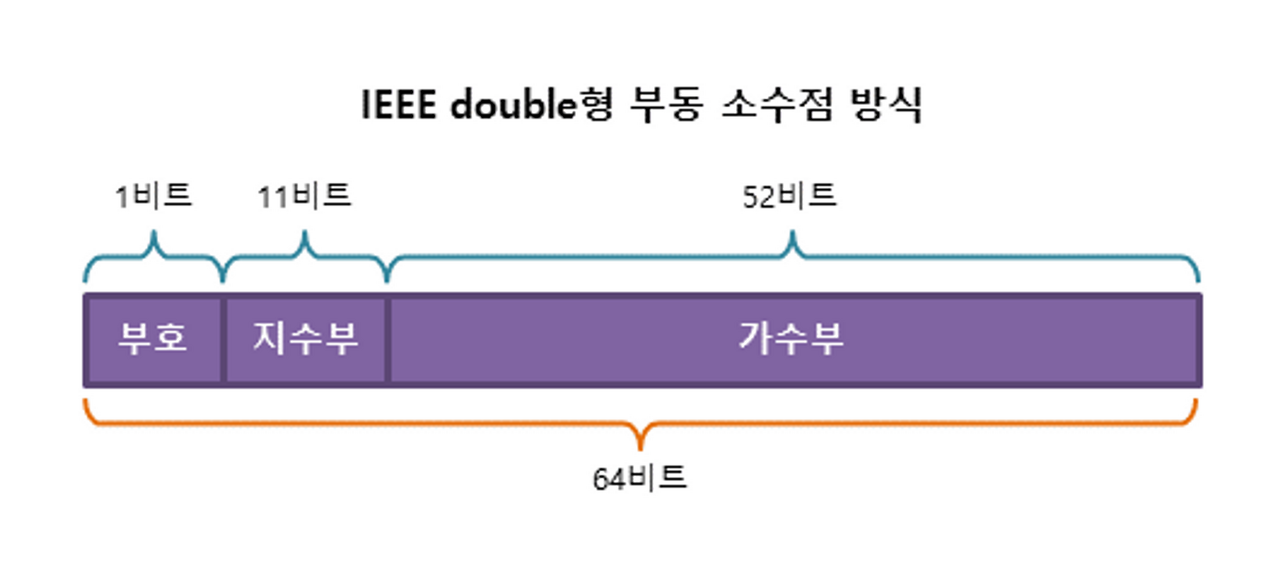
고정 소수점 방식은 제한된 자릿수로 인해 표현할 수 있는 범위가 매우 작음.
→ 하지만 부동 소수점 방식은 위의 수식을 이용하여 매우 큰 실수까지도 표현할 수 있음.
→ 현재 대부분의 시스템에서는 부동 소수점 방식으로 실수를 표현 가능
- 부동 소수점 방식의 오차
- 실수의 부동 소수점 변환

→ 나머지 0이 나왔으니 변환을 종료하고 빼낸 숫자들을 위에서부터 읽어주면 된다.
즉 0.625 → 0.101₍₂₎ 이 된다.
0.5, 0.25, 0.125, 0.75와 같은 숫자들이 2진수로 변환하기 편하고, 반대로 0.789와 같은 숫자는 10진수 기준으로는 자릿수가 길지 않더라도 2진수로 바꾸면 엄청나게 길이가 늘어난다.
'Java > Java의 정석' 카테고리의 다른 글
| [Java의 정석/2-1] 연산자(Operator) (1) | 2023.03.05 |
|---|---|
| [Java의 정석/1-5] 형변환(Casting) (0) | 2023.03.05 |
| [Java의 정석/1-3] 진법 (0) | 2023.03.04 |
| [Java의 정석/1-2] 변수의 타입 (0) | 2023.03.03 |
| [Java의 정석/1-1] 변수(Variable) (0) | 2023.03.03 |

