[TIL-52/240328] 프림(Prim) 알고리즘

TIL

[TIL-52/240328] 프림(Prim) 알고리즘

prao 2024. 3. 29. 00:10

프림 알고리즘

프림 알고리즘이란?

하나의 정점에서 연결된 간선들 중에 하나씩 선택하면서 MST를 만들어 가는 방식

임의의 정점을 선택하여 시작
- 어짜피 모두 연결되므로 임의의 정점을 선택해도 된다
- 그러므로 첫 정점(0번 또는 1번)을 고른다
선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
모든 정점이 선택될 때까지 2번 과정을 반복

서로소인 2개의 집합 정보를 유지

트리 정점: MST를 만들기 위해 선택된 정점들
비트리 정점들: 선택되지 않은 정점들

프림 알고리즘 의사코드

MST-PRIM(G, r)
	FOR u in G.V
    	u.key ← ∞
        u.p ← NULL
    
    r.key  ← 0
    Q  ← G.V
    WHILE Q != 0
    	Q  ← Extract-MIN(Q)
        FOR v in G.Adj[u]
        	IF v

프림 알고리즘 실습

다익스트라(Dijkstra) 알고리즘

다익스트라 알고리즘이란?

시작 정점에서 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식
탐욕 알고리즘 중 하나이고, 프림 알고리즘과 유사
정점 A에서 정점 B까지의 최단 경로(A → X + X → B)

동작 과정

시작 정점 입력
거리 저장 배열을 ∞로 초기화
시작점에서 갈 수 있는 곳의 값 갱신
아직 방문하지 않은 점들이 가지고 있는 거리 값과 현재 정점에서 방문하지 않은 정점까지의 가중치의 합이 작다면 갱신
모든 정점을 방문할 때까지 반복

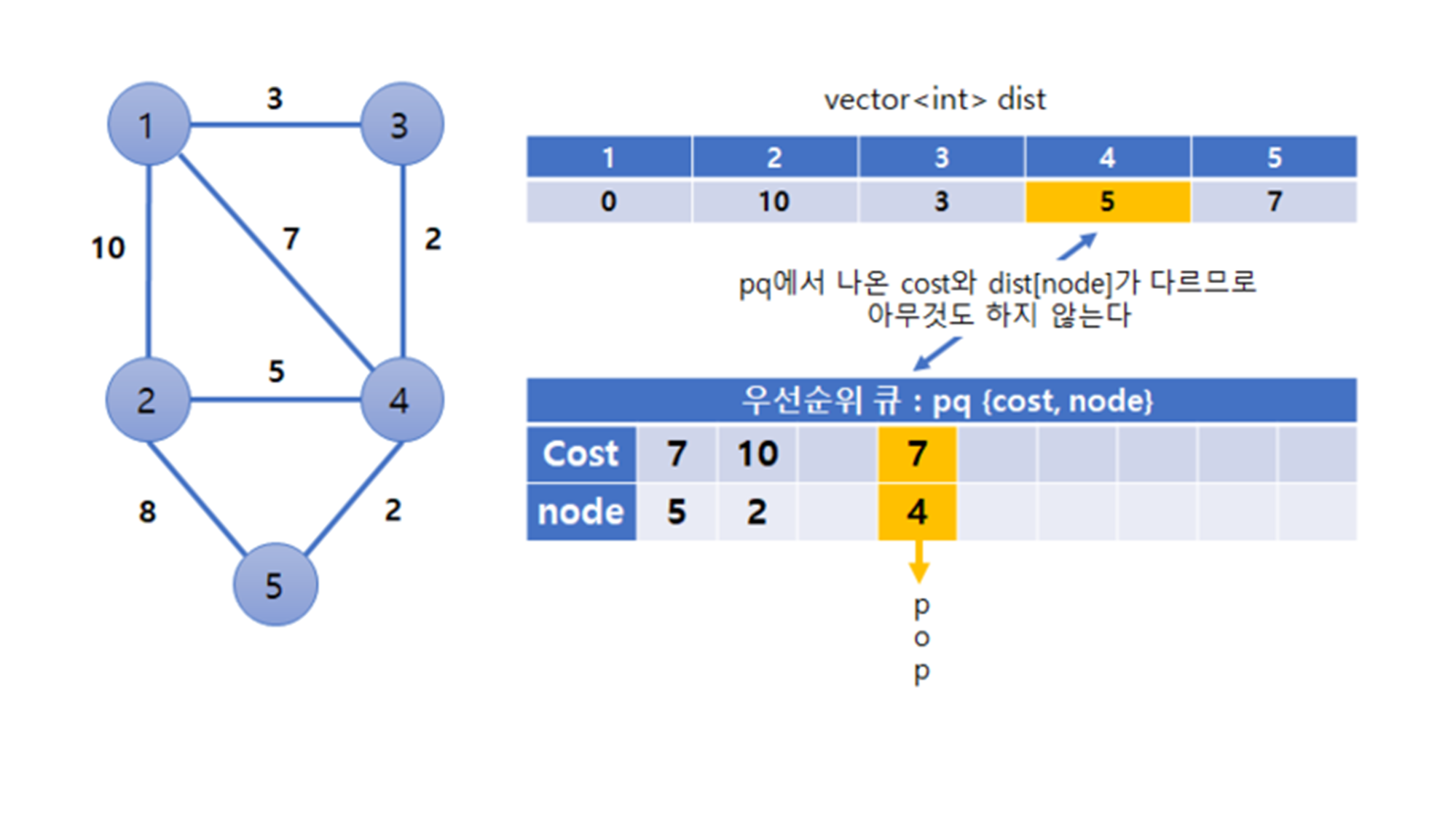
순환 과정 예시

34 순서로 읽으면 된다.

크루스칼 / 프림 / 다익스트라 비교

대표적인 그리디(greedy) 문제
크루스칼, 프림 : 최소 신장 트리(MST)를 만듦
다익스트라, 벨만포드 : 최단거리를 구함

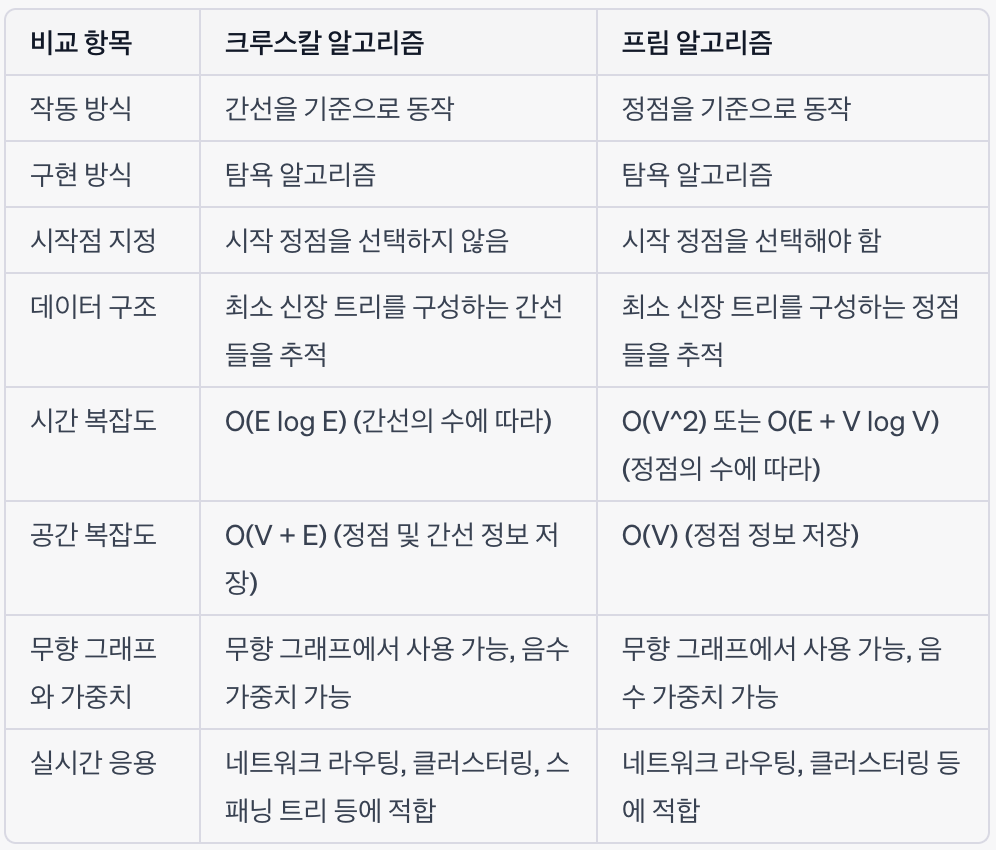
크루스칼 vs 프림, 다익스트라 vs 벨만 포드

그래프에서의 최소 비용 문제

모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리 찾기
두 정점 사이의 최소 비용의 경로 찾기

스패닝 트리

n 개의 정점으로 이뤄진 무향 그래프에서 n개의 정점과 n-1개의 간선으로 이뤄진 트리를 신장 트리라고 함
다른 말로 원래 그래프의 정점 전부와 간선의 부분 집합으로 구성된 부분 그래프
이때 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야 함
이런 특징이 존재하기에 스패닝 트리는 유일하지 않고 여러 개가 존재함
가중치 그래프 여러 개의 스패닝 트리 중 가장 가중치의 합이 작은 트리를 찾는 것이 문제

최소 스패닝 트리(MST)

그래프에서 만날 수 있는 최소 비용 문제 중 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리

크루스칼 알고리즘

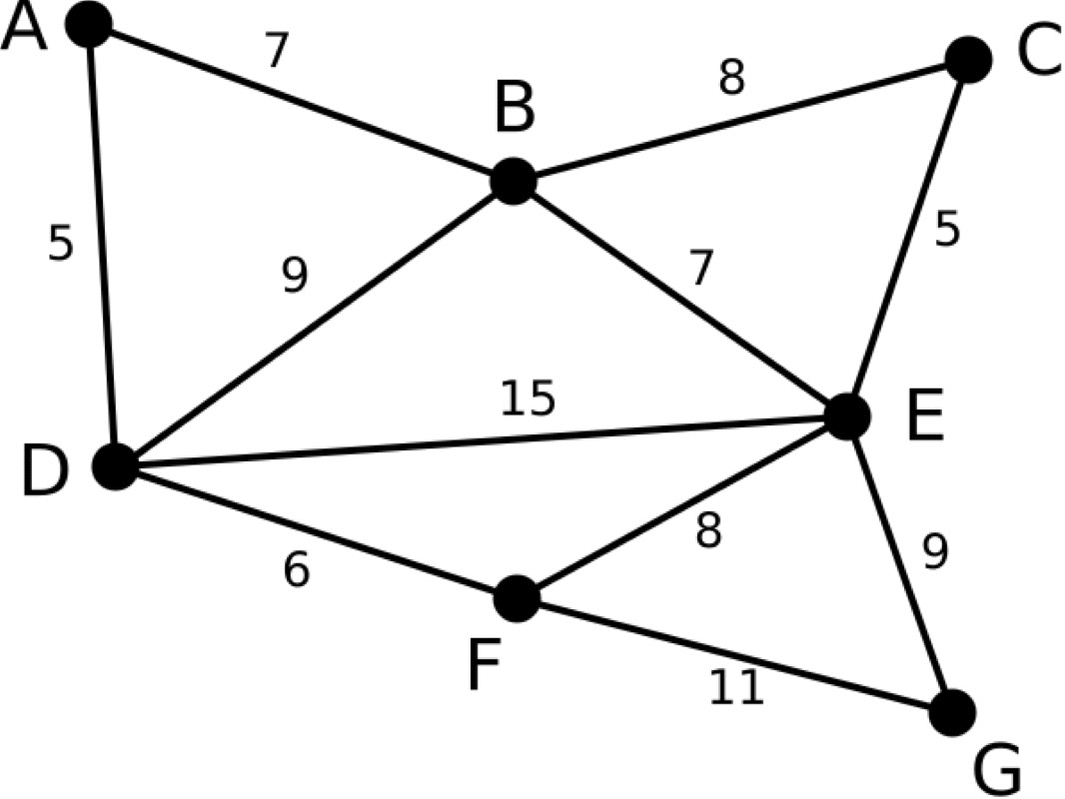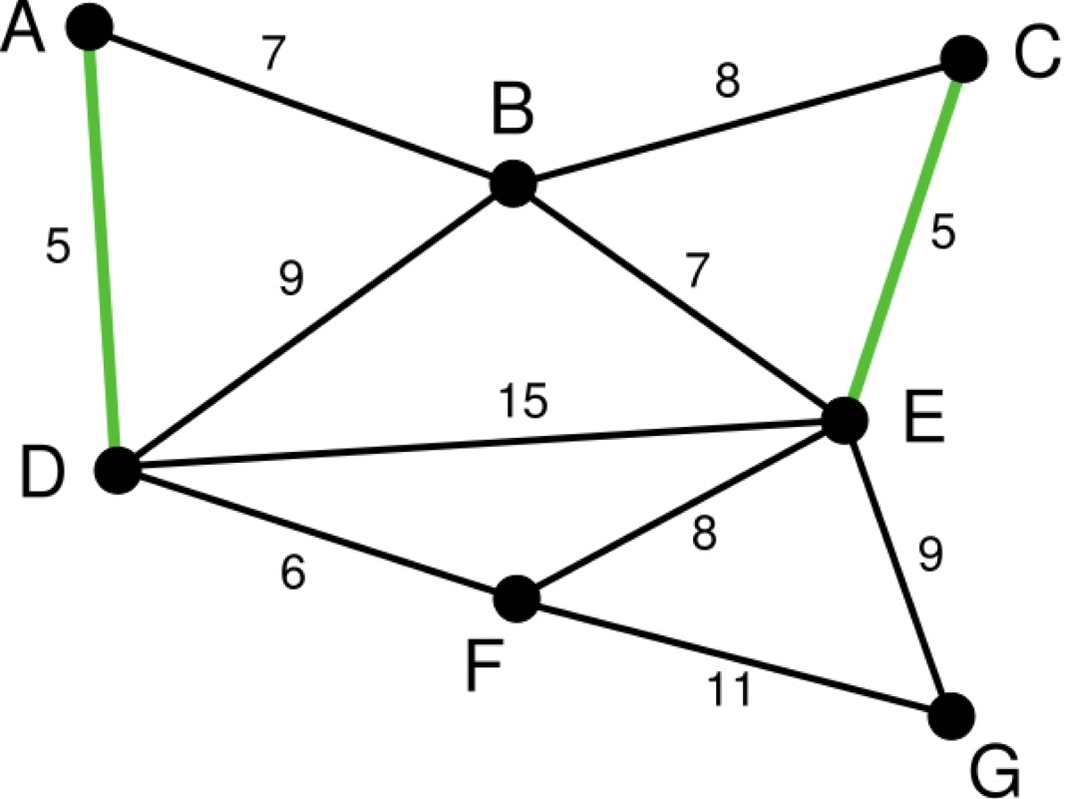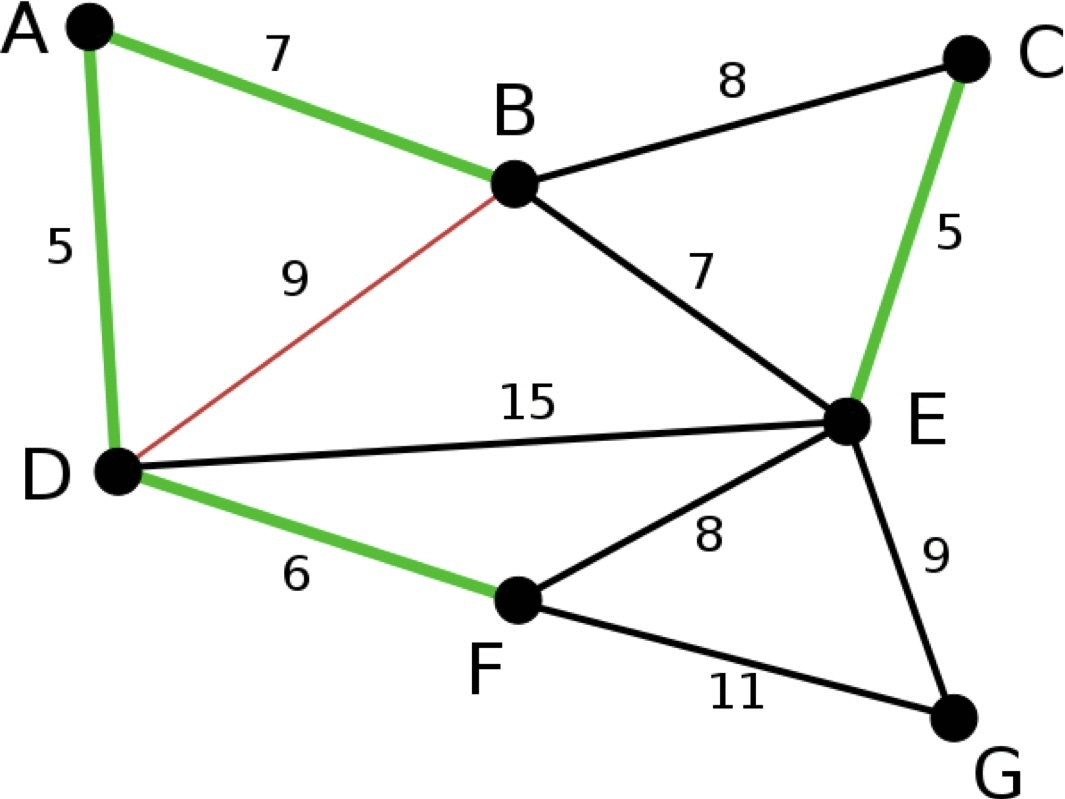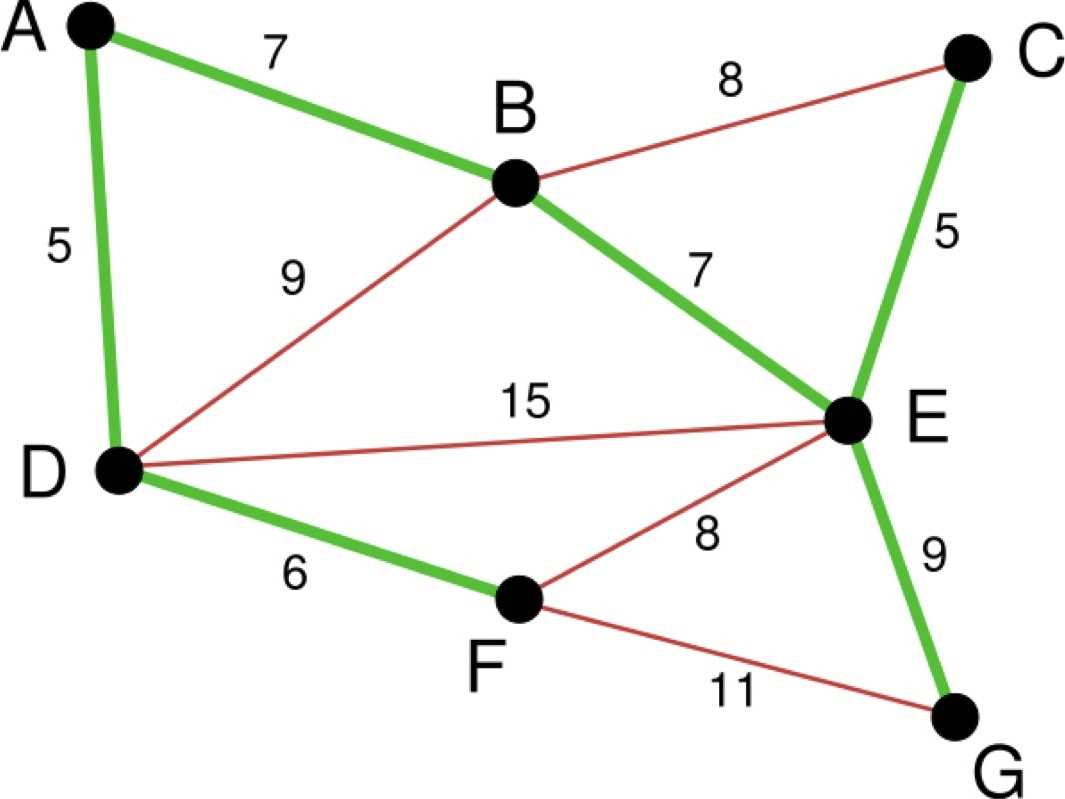
그래프의 모든 간선을 가중치의 오름차순으로 정렬
스패닝 트리에 하나씩 추가(간선들이 사이클을 이루지 않게 해야함)
즉, 사이클이 생기는 간선을 제외한 간선 중 가중치가 가장 작은 간선들을 트리에 추가

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.StringTokenizer;

public class 크루스칼 {

    static class Edge implements Comparable<Edge> {
        int start, end, weight;
        public Edge(int start,int end, int weight){
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
        @Override
        public int compareTo(Edge o){
            return Integer.compare(this.weight,o.weight);
        }
    }
    static int V;
    static int E;
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer st;
    static Edge[] edgeList;
    public static void main(String[] args) throws IOException {
        st = new StringTokenizer(br.readLine()," ");
        V = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());

        edgeList = new Edge[E];
        for(int i = 0;i<E;i++){
            st = new StringTokenizer(br.readLine()," ");
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int weight = Integer.parseInt(st.nextToken());
            edgeList[i] = new Edge(start,end,weight);
        }
        Arrays.sort(edgeList);//오름차순
        make();// 모든 정점을 각각 집합으로 만들고 출발한다.
        //간선 하나씩 시도하며 트리를 만든다.
        int cnt = 0,result = 0;
        for(Edge edge : edgeList){
            if(merge(edge.start,edge.end)){
                result += edge.weight;
                if(++cnt == V-1) break;// 신장트리 완성.
            }
        }
        System.out.println(result);

    }
    static int[] parents;
    static void make(){
        parents = new int[V];
        for(int i = 0;i<V;i++){
            parents[i] = i;
        }
    }
    //u가 속한 트리의 루트 번호를 반환한다.
    static int find(int u){
        if(u == parents[u]) return u;
        //return find(parent[u]); --- 기울어진 트리의 경우 비효율적
        //최적화(Path Compression)
        return parents[u] = find(parents[u]);
    }
    //u가 속한 트리와 v가 속한 트리를 합친다..
    static boolean merge(int u, int v){
        u = find(u);
        v = find(v);
        //u와 v가 이미 같은 트리에 속하는 경우는 걸러낸다.
        if(u ==v) return false;
        parents[u] = v;
        return true;
    }
}

프림 알고리즘

다익스트라 알고리즘과 거의 같은 형태를 띠고 있음
크루스칼 알고리즘이 이곳 저곳에서 산발적으로 만들어진 트리의 조각들을 합쳐서 스패닝 트리를 만든다면, 프림 알고리즘은 하나의 시작점으로 구성된 트리에 간선을 하나씩 추가하는 방식으로 진행됨
따라서 항상 선택된 간선들은 중간 과정에서도 연결된 트리를 만듦
선택할 수 있는 간선들 중 가중치가 가장 작은 간선을 선택하는 과정을 반복

파란색 선: 이번 단계에서 고려할 간선
하늘색 선: 파란색 선 중 선택된 간선
초록색 선: 이미 선택된 간선

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class PrimTest {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        int N = Integer.parseInt(br.readLine());
        int[][] adjMatrix = new int[N][N];
        boolean[] visited = new boolean[N];
        int[] minEdge = new int[N];


        for(int i = 0;i<N;i++){
            st = new StringTokenizer(br.readLine()," ");
            for(int j = 0;j<N;j++){
                adjMatrix[i][j] = Integer.parseInt(st.nextToken());
            }
            minEdge[i] = Integer.MAX_VALUE;
        }

        int result = 0;//최소 신장 트리 비용
        minEdge[0] = 0;//임의의 시작점 0의 간선 비용을 0으로 세팅 index는 아무거나 상관없다.
        for(int i = 0;i<N;i++){
            // 1. 신장 트리에 포함되지않은 정점 중 최소간선비용의 정점 찾기
            int min = Integer.MAX_VALUE;
            int minVertex = -1;//최소간선비용의 정점번호
            for(int j = 0;j<N;j++){
                if(!visited[j] && min>minEdge[j]){
                    min = minEdge[j];
                    minVertex = j;
                }
            }
            visited[minVertex] = true;//신장트리에 포함시킴.
            result += min;//간선비용 누적.

            //2. 선택된 정점 기준으로 신장트리에 연결되지않은 타 정점과의 간선 비용 최소로 업데이트
            for (int j = 0; j < N; j++) {
                //인접 안해있으면 인풋이 0이므로 걔가 최소가 되어버림.
                if(!visited[j] && adjMatrix[minVertex][j]!=0 && minEdge[j] > adjMatrix[minVertex][j]){
                    minEdge[j] = adjMatrix[minVertex][j];
                }
            }
        }
        System.out.println(result);
    }
}

크루스칼 vs 프림
크루스칼 : 간선 위주 / 프림 : 정점 위주
이미 만들어진 트리에 인접한 간선을 고려하는지의 여부를 제외하면 완전히 똑같은 알고리즘

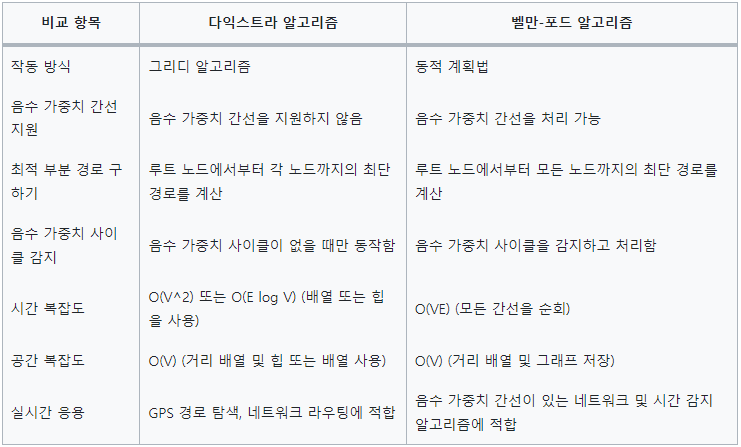
최단 경로 알고리즘

하나의 시작 정점에서 끝 정점까지의 최단 경로 구하기
1. 다익스트라 알고리즘 : 음의 가중치 허용 x(그리디 적용 가능)
2. 벨만-포드 알고리즘 : 음의 가중치 허용
모든 정점들에 대한 최단 경로
1. 플루이드-워셜 알고리즘

다익스트라

한 시작 정점이 주어졌을 때 그 정점에서 다른 정점으로의 최단 경로를 구하는 알고리즘

//init
S = {v0}; distance[v0] = 0; 
for (w 가 V - S에 속한다면)//V-S는 전체 정점에서 이미 방문한 정점을 뺀 차집합.
	if ((v0, w)가 E에 속한다면) distance[w] = cost(v0,w); 
	else distance[w] = inf;

//algorithm
S = {v0};
while V–S != empty {
  //아래의 코드는 지금까지 최단 경로가 구해지지않은 정점 중 가장 가까운 거리를 반복한다는 의미
	u = min{distance[w], w 는 V-S의 원소};//---1
	
  S = S U {u}; 
  V–S = (V–S)–{u};
	for(vertex w : V–S)
		distance[w] = min{distance[w],distance[u]+cost(u,w)}//update distance[w];---2
}

다익스트라 알고리즘 로직(우선순위 큐)

첫 번째 정점을 기준으로 연결되어있는 정점들을 추가해가면서 최단 거리를 갱신
꺼낸 노드는 다음의 과정을 반복합니다.
1. 첫 정점을 기준으로 배열을 선언핸 첫 정점에서 각 정점까지의 거리를 저장
  - 초기에는 첫 정점의 거리를 0, 나머지는 무한대(inf)로 저장
  - 우선순위 큐에 순서쌍 (첫 정점, 거리 0) 만 먼저 넣음
2. 우선순위 큐에서 노드를 꺼냄
  - 처음에는 첫 정점만 저장된 상태이기때문에 첫번째 정점만 꺼내짐
  - 첫 정점에 인접한 노드들 각각에 대해 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장된 첫 정점에서 각 정점까지의 거리를 비교합
  - 배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧은 경우, 배열에 해당 노드의 거리를 업데이트
  - 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 해당 노드를 넣음
3. 2번의 과정을 우선순위 큐에서 꺼낼 노드가 없을 때까지 반복

다익스트라 구현

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;

public class BOJ_1753 {
	
	// INF 값 초기화
	static final int INF = 9999999;
	// 그래프를 표현 할 2차원 List
	static List<List<Node>> graph = new ArrayList<>();
	// 최단거리테이블을 표현 할 배열
	static int[] result;
	// 방문처리를 위한 배열이지만 저는 다른 방법으로 방문처리를 진행하겠습니다.
	//	static boolean[] vistied;

	public static void main(String[] args) throws IOException {
		
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
	
		String[] info = br.readLine().split(" ");
		int startIndex = Integer.parseInt(br.readLine());
		
		// 그래프 생성
		for (int i = 0; i < Integer.parseInt(info[0])+1; i++) {
			graph.add(new ArrayList<>());
		}
		// 최단거리테이블 생성
		result = new int[Integer.parseInt(info[0])+1];
		// 최단거리테이블 INF로 초기화
		Arrays.fill(result, INF);
		
		// 방문처리를 위한 배열 생성 (저는 사용하지 않습니다)
		// vistied = new boolean[Integer.parseInt(info[0])+1];
		
		// 문제에서 주어진 입력 값에 따라 그래프 초기화
		for (int i = 0; i < Integer.parseInt(info[1]); i++) {
			String[] temp = br.readLine().split(" ");
			graph.get(Integer.parseInt(temp[0])).add(new Node(Integer.parseInt(temp[1]), Integer.parseInt(temp[2])));
		}
		
		// 문제에서 주어진 입력값을 바탕으로 다익스트라 알고리즘 수행
		dijkstra(startIndex);
		
		// 문제에서 제시한 조건에 맞게 출력
		for (int i = 1; i < result.length; i++) {
			if(result[i] == INF) {
				bw.write("INF");
				bw.newLine();
			}else {
				bw.write(String.valueOf(result[i]));
				bw.newLine();
			}
		}
		bw.flush();
		
	}
	
	// 다익스트라 알고리즘
	static void dijkstra(int index) {
		
		// 최단거리가 갱신 된 노드들을 담을 우선순위 큐 생성
		PriorityQueue<Node> pq =  new PriorityQueue<>();
		// 최단거리테이블의 시작지점노드 값 0으로 갱신
		result[index] = 0;
		// 우선순위 큐에 시작노드 넣기
		pq.offer(new Node(index, 0));
		
		// 우선순위 큐에 노드가 존재하면 계속 반복
		while(!pq.isEmpty()) {
			// 큐에서 노드 꺼내기
			Node node = pq.poll();
			// 꺼낸 노드의 인덱스 및 최단거리 비용 확인
			int nodeIndex = node.index;
			int distance = node.distacne;
			
			// 앞에서 주석처리했던 방문처리 배열을 사용해서 아래와 같이 방문처리하셔도 됩니다.
//			if(vistied[nodeIndex]) {
//				continue;
//			}else{
//				vistied[nodeIndex] = true;
//			}
			
			// 큐에서 꺼낸 거리와 최단거리테이블의 값을 비교해서 방문처리를 합니다.
			// 큐는 최단거리를 기준으로 오름차순 정렬되고 있습니다.
			// 만약 현재 꺼낸 노드의 거리가 최단거리테이블의 값보다 크다면 해당 노드는 이전에 방문된 노드입니다.
			// 그러므로 해당노드와 연결 된 노드를 탐색하지 않고 큐에서 다음 노드를 꺼냅니다.
			if(distance > result[nodeIndex]) {
				continue;
			}
			
			// 큐에서 꺼낸 노드에서 이동 가능 한 노드들을 탐색합니다.
			for (Node linkedNode : graph.get(nodeIndex)) {
				// 해당노드를 거쳐서 다음 노드로 이동 할 떄의 값이 다음 이동노드의 최단거리테이블 값보다 작을 때
				if(distance + linkedNode.distacne < result[linkedNode.index]) {
					// if문의 조건을 만족했다면 최단거리테이블의 값을 갱신합니다.
					result[linkedNode.index] = distance + linkedNode.distacne;
					// 갱신 된 노드를 우선순위 큐에 넣어줍니다.
					pq.offer(new Node(linkedNode.index, result[linkedNode.index]));
				}
			}
		}
	}
	
	// 우선순위 큐에서 정렬기준을 잡기위해 Comparable를 구현합니다.
	static class Node implements Comparable<Node>{
		int index;			// 노드 번호
		int distacne;		// 이동 할 노드까지의 거리

		Node(int index, int distacne) {
			this.index = index;
			this.distacne = distacne;
		}
		
		// 최단거리를 기준으로 오름차순 정렬합니다.
		@Override
		public int compareTo(Node o) {
		return Integer.compare(this.distacne, o.distacne);
		}
	}
	
}

저작자표시 비영리 변경금지